Christmastide Puzzles - Solutions Reveal, Top Solvers, and More...
The Christmas-New Year Solving contest, where we posed our readers with six unconventional and engine-defying problems to solve, came to a close on the 31st of December. The event became a grand success bringing in some very high-class competition. We received around 65 emails in all, a surprising majority of which were accompanied by extremely well-written and well-explained solutions. Of course, too many perfect 50-out-of-50 scorers left us in a quandary. The solvers posed us a seventh problem, as it were: whom to choose? whom to leave? But after some discussion and pondering, we think we too have found the best solution!
Who, dear friends, doesn't enjoy some good old-fashioned puzzling? Isn't the human mind innately drawn to conundrums and mysteries? Yet, growing up, somehow it is often the case that men lose this singular disposition to analyse and reason. Over the years they seem to fall into lazy patterns of thought and tend to excuse themselves out of every exercise that might tax their faculties of discernment and reckoning. "Crime is common," as Sherlock Holmes would say, "the logic is rare," but part of the reason why it is so is the rote and formal ways of the education system one is brought up in; problem solving, when it puts on the mantle of theory and abstraction, almost invariably ceases to be any fun. However, evolutionarily speaking, the brain is indeed meant to exult as much in the act of unravelling and hypothesizing as muscles and sinews in the exhibition of physical strength and flexibility.

Our aim with this Christmastide solving contest was to exhort you to revert to that natural analytical self of yours, to fire those neurons under your temples, and boy, did we succeed! At the time of publishing the first article we honestly hoped for not more than a dozen entries, and that's the reason we didn't bother to put a tiebreaker in place, but by the time the curtains came down on the final few moments of 2020, teamchessbaseindia@gmail.com was spilling with emails. We received around 65 emails, not just from within India, but also from various parts of the world - Germany, Romania, Russia, USA - to name a few! And what was perhaps even more surprising was the outstanding quality of these entries. At least 17 of them had perfect solutions, and at least twice more than that scored more than fifty percent. In a sense, it was a sort of a confluence, as it was not only chess players, but also solvers and composers who took part in the event, and from the answers one could see that the participants were of varied strengths and from various backgrounds.



A few of the participants were presumably somewhat new to problem chess, they were probably coming across stipulations such as selfmates or helpmates for the very first time. But they did a commendable job of researching and making up for their lack of experience.

Some of them even decided to work in teams, the name of Sachin Samant comes to mind, who solved all six of the problems jointly with his daughter and son, Ruchira and Aditya. How adorable is that? Who would have ever guessed that solving chess problems could fit in so well with spending time with family during the holidays!
We also had a lot of experts sending in solutions. There was at least one titled player, the young International Master, Neelash Saha. There were also some of the well-known composers like Alexey Gasparyan, Ralf Kratschmer, and S. Manikumar joining in. But, from this rather variegated lineup, who were the ones who came out on the top? We will get to that soon, before that let us officially reveal the solutions to all the six problems.
The Solutions
Section (I): Adversarial Problems
You would be pleased and surprised to know that the originals in this section were by a 17-year-old high-school student! Meet James Malcom, the creator of the selfmate and the 76-move long castling problem! He lives in Iowa, USA, and just like chess enthusiasts his age, loves playing online games. But he is different in one aspect, he also takes a lot of pleasure in composing and is especially fond of record tasks, jokes, and anything related to the three special moves of chess: castling, promotion, and en passant. A very uncommon interest for a young man!

Now let's tackle his compositions one by one, shall we? They weren't difficult to solve but they were, as several of our participants jubilantly pointed out, every bit amusing and clever, just like Christmas puzzles should be!
Problem #01

16-moves sounds too long, but this is rather easy once you get the idea! White's king is already in its deathbed and a knight needs to be sacrificed on g6 to make hxg6# happen. Black's only mobile piece is that bishop on h2, White would like to keep it the same way, disturb very little in the position and carry out Ng6+ hxg6# at the right moment. A white pawn must therefore promote to a knight, and additionally, one more unit is needed to block e4, the white king's only available escape, suggesting that wPd2 must also be freed and promoted.
1.a4 Bg1 2.a5 Bh2 3.a6 Bg1 4.a7 Bh2 5.a8=B we have our self-blocker and also the piece which would free wPd2! 5...Bg1 6.Be4 Bh2 7.Bxd3 Bg1 8.Be4 Bh2 9.d4 Bg1 10.d5 Bh2 11.d6 Bg1 12.d7 Bh2 13.d8=N now take a knight, as planned, 13...Bg1 14.Nc6 Bh2 15.Ne7 Bg1 16.Ng6+ hxg6# - done, nice and easy!
Problem #02

If it was Black's turn in this position, Black wouldn't be able to move the b1 knight, because 1...Na3 or 1...Nd2 allows White to castle in the next move, and so does 1...Nc3 2.Nxc3. Similarly, with White to move, moving the e2 knight doesn't make sense as that would enable Black to maneuver Nc3-Nd1 etc. Hence, logically, 1.Be8! should be the first move, but how does this help?
1.Be8 Kg8 2.Bd7 Kh8 3.Bc8 Kg8 4.Bb7 Kh8 5.Ba6 Kg8 6.Bc8 Kh8 note that 4.Ba6 5.Bb7 6.Bc8 too leads to exactly the same thing - a harmless triangulation dual! 7.Bd7 Kg8 8.Be8 Kh8 9.Bf7 and now Black is forced to push one of the pawns, let's say, 9...a4; so once again White goes 10.Be8, 11.Bd7, and 12.Bc8 followed by triangulation, forcing Black yet again to move another pawn.
This continues nine times, totalling 9x7=63 moves, until Black's pawns run out of play and the following position is reached:

From above White carries out one last round of bishop triangulation: 64.Be8 Kg8 65.Bd7 Kh8 66.Bc8 Kg8 67.Bb7 Kh8 68.Ba6 Kg8 69.Bc8 Kh8 (or 67.Ba6 68.Bb7 69.Bc8) 70.Bd7 Kg8 71.Be8 Kh8 72.Bf7 and here finally Black is compelled to move the b1 knight and after 72...Nc3 73.Nxc3 e2 74.Bg8 Kxg8 (or 74.Be8 Kg8, another minor dual!) 75.Nxe2 Kh8 White goes 76.0-0-0 - et voila!
Note how the line sketched above is optimal, Black keeps the knight posted on b1 for as long as possible. Had it moved earlier, White would have obviously castled quicker. Still have doubts? Well, then replay the sample 76-move variation below:
James dedicated the above to his good "composing buddy", the German International Master of chess composition Arno Tüngler. Tüngler specializes in fairy problems nowadays and has registered some amazing successes composing series-helpmates lately. James's penchant for setting up record tasks is evident in the above creation, see below how he has also found a way to extend this idea to 85 moves. It would really be interesting to see if any of our readers can exceed this figure!

Section (II): Cooperative Problems
Problem #03

The above was a joint effort of the Ukrainian-Israeli composer Leonid Lyubashevsky and the well-known book-author Sergei Tkachenko. As is the case with all long problems featuring help-play, the trick here is to visualize the final position.

1.Kh3 Ba2 2.Kg2 Bb1 3.Kf1 Ba2 4.Ke1 Bb1 5.Kd1 Ba2 6.Kc1 Bb1 7.Kb2 Ba2 8.Kxa1 the knight defending the c2 square must be eliminated to make progress 8...Bb1 9.Kb2 Ba2 10.Kxc2 Bb1+ 11.Kxb3 Bxe4 12.Kxc4 Bxf5 13.Kd5 Bd3 14.Kxe6 Bf1 15.Kf5 Bh3# - after so much roving, the black monarch finally rests in piece!
Problem #04

This is another delightful problem. Lengthy but hardly difficult, as often such problems are. The pawn on c4 is the impediment here, impediment to the obvious c3-c4# - that is all one needs to observe, the rest is self-evident:
1.b1=B 2.Bc2 3.Bd1 4.Be2 5.Bf1 6.Bh3 7.Bg4 8.Bh5 9.Be8 10.Bd7 11.Bc8 12.Ba6 13.Bxc4 14.Ba6 15.Bc8 16.Bd7 17.Be8 18.Bh5 19.Bg4 20.Bh3 21.Bf1 22.Be2 23.Bd1 24.Bc2 25.Bb1 and thus enabling 25...c4# - A wonderful product of collaboration between a highly-experienced contemporary composer, Paz Einat, and the Hungarian legend, György Bakcsi, who passed away in 2019.
Section (III): Proof Games and Path Enumerations
Problem #05

The composers: Joost de Heer, Gianni Donati, and Michel Caillaud - are all acclaimed names in the world of Proof Games and Retroanalysis. This, as was mentioned in the first article, is an all-time favourite of the author of this article. You will know why once you see the solution!
White has only seven moves to reach the given position and that's actually the quickest that can be done, and yet... 1.a3! e6 2.Ra2! Bxa3 3.Rxa3 f6! 4.Rh3 f5 5.Rh6 Nxh6 6.h3! Rf8 7.h4 Ng8 ...yet, White must lose as many as four tempos along the way! I haven't seen a better, a more impossible example of the so-called "Festina lente" paradox. You must make haste, as they say, but slowly!
The most important problem of this contest, the problem that carried the maximum points, was a handiwork of our good friend and chief adviser in matters of Retrograde Analysis, Andrew Buchanan!

Andrew Buchanan is an itinerant IT consultant, currently living and working in Singapore, who has been interested in chess problems, principally retros, since 2001. He is particularly noted for developing the curious concept of Dead Reckoning in retro chess. You will find a wealth of material on this on his own website here.
Problem #06

So, for this last problem, there are multiple ways to reach the given position in the stipulated number of moves, and you have to count exactly how many such sequences are there. 1. f4 Na6 2. f5 Nb4 3. f6 Nxa2 4. fxg7 Nxc1 5. gxf8=B c6 6. Bxe7 Qb6 7. Bh4 Nb3 8. Bf2 Nxd2 9. e3 Qb3 10. Ne2, for instance, is a possible sequence. But how can this vary? Well, there isn't scope for many variations here. Firstly, for counting Black's moves, we need to consider that Black may start with 1...Nc6 instead of 1...Na6, giving us two broad cases to deal with; and secondly, for White's moves, we have to account for the various routes the pawn on f2 takes to promote and then carry out a Rundlauf. The counting won't be too complicated because, for our benefit, White's and Black's moves are all independent of each other.
Counting Black's moves:
Case (i) Black starts the knight with Nc6: In this case, the first two moves must be Nc6 and Nb4. c6 and Qb6 can only follow later. But again, Qb6-b3 can only happen after Nb3xd2. So in between Nc6-Nb4 and Qb3 we have six moves. And the two strings, Na2 > Nc1 > Nb3 > Nd2 and c6 > Qb6, combine in C(6,2) = 15 ways.
Case (ii) Black starts the knight with Na6: In this case, the strings Na6 > Nb4 > Na2 > Nc1 > Nb3 > Nd2 and c6 > Qb6 are independent and combine in C(8,2)=28 ways. Hence, the net number of Black moves turns out to be 15+28 = 43.
Counting White's moves:
Case (i) The f2 pawn went fxg7 and gxf8=B returning via Be7-Bc5-f2: In this case e3 must happen after Bf2. So there can be just one sequence: 1. f4 2. f5 3. f6 4. fxg7 5. gxf8=B 6. Bxe7 7. Bc5 8. Bf2 9. e3 10. Ne2
Case (ii) The f2 pawn went fxe7 and exf8=B returning via Bg7-Bd4-Bf2: In this case again e3 must happen after Bf2. So there's only one sequence, namely 1. f4 2. f5 3. f6 4. fxe7 5. exf8=B 6. Bxg7 7. Bd4 8. Bf2 9. e3 10. Ne2
Case (iii) The f2 pawn (after fxg7 and gxf8=B) returned via Be7-h4-f2: In this case e3-Ne2 can happen any time, hence we combine f4 > f5 > f6 > fxg7 > gxf8=B > Bxe7 > Bh4 > Bf2 and e3 > Ne2, and that can be done in C(10, 2)=45 ways. Therefore, total sequences for White = 45+2= 47
The above cases clearly exhaust all possibilities, and hence the total number of sequences (or games) reaching the given position simply is 43x47=2021. A perfect problem and a perfect way to wish a happy new year 2021! Since, 43 and 47 are two delightfully manageable prime factors, a few of our solvers eschewed the use of combinatorics and adopted a somewhat brute-force approach; among these, there was even a 12-year-old!


And here's a fun-fact we came to know about 2021 on the internet:
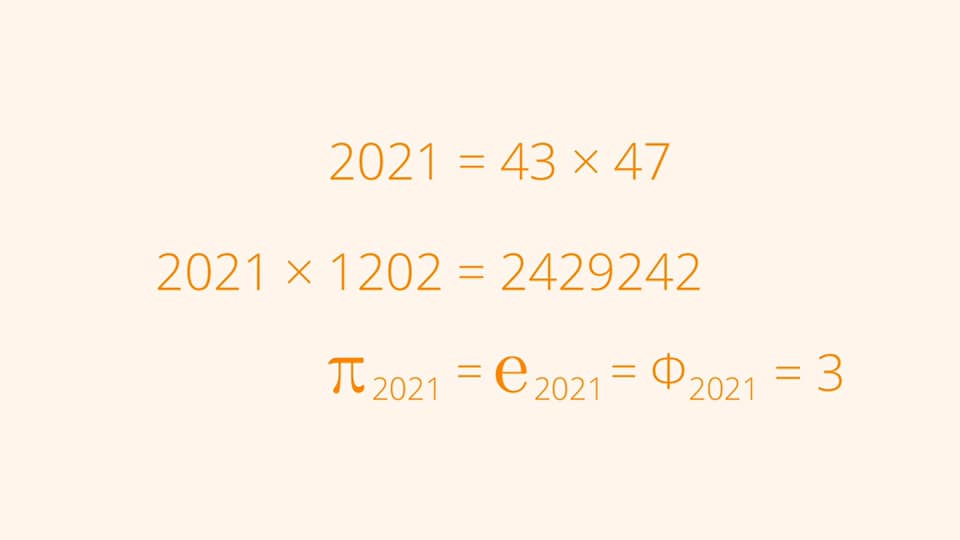
Now it's time to reveal the solvers extraordinaire!!
Like it has been mentioned, the competition was exceptionally high. We were literally overwhelmed with responses flooding in...

But seriously, after much hemming and hawing, we could shortlist the following candidates as better from the rest:
1.Neelash Saha
2.Sayan Roy
3.Sachin Samant / Samant Family (Aditya, Ruchira, and Sachin)
4.Adil Tanveer
5.Alekhya Mukhopadhyay
6.Rohit Shelke
7.Sourath Biswas
8.Soham Bhattacharya
9.Anirudh Daga
10.Velmurugan Nallusamy
11.Udit Kamdar
12. Umang Kamdar
13.Sethu Madhav Upadhyayula
14.Parmar Tiharbhai Rameshbhai
15.Dr.S.Manikumar
16.Jochen Wege
17. Piyush Narsikar
What this competition has proved beyond doubt is that people do appreciate intelligent and out-of-the-box content, and most importantly, the rift between problem and over-the-board chess is nothing but superficial. Apart from the sixteen solvers above, there were plenty others who missed perfection only narrowly. Debdeep Paul, for instance, had sent an excellent mail, but for some reason, didn't provide satisfactory explanation for the second problem. Wilfried Neef, sent a heartwarming message from Germany with impeccable solutions, but didn't show the math for the last problem. Ralf Kratschmer and Alexey Gasparyan, the composers who took part, skipped the mathematics as well, which is why they do not appear in the above list.
It goes without saying that we are much obliged to each every participant who contributed to making this one of a kind event a success. However, if inadvertently we have missed any one of you sifting through 60+ emails, and if you think you did solve all the six problems correctly and weren't mentioned above, then do write to us and we will look into it.
The Hunt for the Top three will continue...
The prize winners still remain undecided, and to sort that out we have decided to conduct a live quiz with IM Sagar Shah as the host on ChessBase India YouTube. The top solvers will receive invitations very soon and the details will be communicated to them privately!















































