Winter Solving: Solutions Reveal, Top Solvers, and More...
The two tiers of the ChessBase India Winter Solving Championship concluded on December 11, 2023. The event was a resounding success, receiving over 70 entries from all over the world, not just India, and witnessing participation from diverse backgrounds and age groups. There were titled players and solvers as well as skilled amateurs. And there were students and teenagers as there were adult professionals. The level of competition was outstanding. With much difficulty, we have selected a list of best scorers from the many high-quality answers we received. We have planned a tiebreaker between these contestants next week. In this report, we give you the details of the same and, of course, reveal the solutions to the 12 problems we posed.
First things first, here is our (tentative) list of the top scorers:
1. Alexandru Mihalcescu (90)
2. Joachim Hambros (90)
3. Vlaicu Crisan (90)
4. Juha Saukkola (90)
5. Pracheta Agarwal (90)
6. Személyi Sebestyén (90)
7. Sayan Roy (90)
8. Sethu Madhav Upadhyula (90)
9. Balázs Személyi (90)
10. Vivaan Saraogi (90)
11. Stephen Rome Pangilinan (85)
12. Bharath Thanigaivelan (85)
13. Swati Mohota (82)
14. Velmurugan Nallusamy (82)
The above are the names of all those participants who have scored more than 90 per cent in the two tiers of the competition combined, that is, more than 81 out of 90. The first ten participants have scored a perfect 90/90. Stephen Rome Pangilinan and Bharath Thanigaivelan solved the first reflexmate problem of the first tier incorrectly and missed five points. As we will see, they found the "try" 1. Qa8 instead of the key 1. Qf1. The rest of their answers were impeccable. Swati Mohota took a brute-force approach to the path enumeration problem in the second tier, but her calculation fell short of the actual number by just six. She counted 2017 solutions to the one-sided proof game, but as we establish later in this article, some simple math shows it to be 2023. We awarded Swati Mohota four points for her efforts out of the possible twelve in that problem. Lastly, Velmurugan Nallusamy could only provide partial answers to the helpmates in tier I. He lost 8 points for that and narrowly made the cut. His remaining solutions were all spot on.
Notably, the path enumeration problem eliminated several strong contestants, including quite a few titled players, who supplied spotless answers for all the chess questions but, coming to this counting riddle, missed the mark completely! We have planned a tiebreaker to select the three winners out of the fourteen above. This will take place live on ChessBase India YouTube on January 14th (second Sunday of the year) at 2 pm IST. The finalists will be sent a confirmation email before the event. More on this later in the article.
Let us now delve into the solutions to the 12 problems. Please go through them carefully. If you are one of the participants reading this and think you scored more than 90% and should be included in the list, please write to us at chessbaseindiasocial@gmail.com. We will review your answers and update the list above as needed.
The Solutions
Tier - I
Problem 01
Emanuel Navon, Subotica Internet Composing 2009, 1st Prize

Created by the Israeli IM of chess composition, Emanuel Navon, the majority of the participants solved this first helpmate successfully. The play in a helpmate is simple—the pieces are in a cooperative relationship with one another; there are, as such, no threats or defences to calculate—and the trick comes down to visualising the final mating positions correctly. It seems our solvers were able to do just that without much difficulty! The target squares for the black king are b5 and d5. One of the solutions goes 1. Nc4 Kxc2 2. Kb6 Rd7 3. Kb5 Rb7#. Notice how Black selfpins the b6 knight on c4 to facilitate the checkmate with the rook on b7. This same "anticipatory selfpin" effect is echoed in the other solution but with the c6 knight; moreover, the bishop goes around to b7 this time to deliver the coup de grace: 1. Nd4 Kxc3 2. Kc6 Bxa6 3. Kd5 Bb7#. Two perfectly analogous solutions! The problem also shows the popular theme framework known as the Orthogonal Diagonal Transformation (ODT). Observe that the strategic effects that appear on orthogonal lines in one solution repeat in the other but on diagonal lines, and vice versa.
Problem 02
Hiroaki Maeshima, The Problemist, 2023

If they had it easy with the first helpmate, the second one made their life difficult. Many solvers, including one of the perfect scorers, reported this helpmate in 5 as the toughest problem of the first tier!
Hiroaki Maeshima from Japan is a talented newcomer in the chess composing world. He was initially a chess player but got into composition during the pandemic era in 2020 when there were few tournaments to play at. Since then, he has composed about 60 problems! His main idea in the above problem was to show the beauty and paradox of a tempo move. "A tempo move is a move which can be skipped without any change in the solution lines," says Hiroaki. "I would be happy if solvers find it humorous that when two players work together to checkmate a king, they have to skip a move!"
Here are the solutions: (a) 1. Ke6 dxe3 2. Nd2 Kb6! 3. Nc4 bxc4 4. b3 c5 5. Kd5 Bxb3# and (b) (Nf3 moved to f4) 1. e2 Kc4 2. e3 dxe3 3. Nd5 Kd3 4. e1=B! Ke2 5. Ke4 Bb1#. Needless to say, the tempo moves that Hiroaki alludes to are 2... Kb6 and 4. e1=B.
Problem 03
Byron Zappas, The Problemist 1985, 1st Prize

The easiest way to compel Black to mate the white king is to move Qa4 somewhere where it can't defend e4 and then play Be4, forcing Qxe4#. But the question is, where to move the queen? Something like 1. Qa1, threatening 2. Be4+ Qxe4#, seems convincing, especially when you see that 1... Nxc6 runs into 2. Nb4 Nxb4#, 1... Rb7 into 2. Bb5+ Rxb5#, and 1... Rxc6 into 2. Nc5+ Rxc5#. But can you see the problem with a move like 1. Qa1? It is refuted by 1... Nf6!, which ensures that now Be4+ can be met with Nxe4.
The key, therefore, is 1. Qxf4!, selfpinning the queen! The threat is the same, 2. Be4 Qxe4#, but now 1... Nf6 is met with 2. Qe4+ Nxe4#. The rest of the variations are as follows:
1... Rxc6 2. Nc5+ Rxc5#;
1... Rb7 2. Bb5+ Rxb5#;
1... Nxc6 2. Nb4+ Nxb4#;
1... Bf6 2. Qd4 Bxd4#;
1... Bf7 2. Qc4+ Bxc4#
This was a brainchild of the legendary Greek Grandmaster of chess composition, Byron Zappas. Most solvers were able to solve it, but a few either failed to see the defense 1... Nf6 or didn't know how to deal with it.
Problem 04
Valery Nikolayevich Karpov, Odessa Chess Club 1967, 3rd Prize

This was perhaps the most logical and intuitively clear problem of tier I. The solution begins with the waiting move 1. Rb8! Even without calculating the rest, it makes sense to put the white rook on the intersection of the lines b1-b8 and h2-b8, for the checkmate would likely be delivered on the b8 square either by the b2 rook or the h2 bishop. The following pair of well-matched variations realises this intuition: for 1... c5, we have 2. Ka8 c4 3. Na7 c3 4. Ne6+ Rxb8#, and 1... c6 is met with 2. Nc7 c5 3. Na8 c4 4. Nh7+ Bxb8#. In both cases, White cleverly completes the mating net by putting their knight on a7 and king on a8, and vice versa. A lucid creation!
Problem 05
Friedrich Chlubna, Die Schwalbe 1969, 2nd Hon. Mention
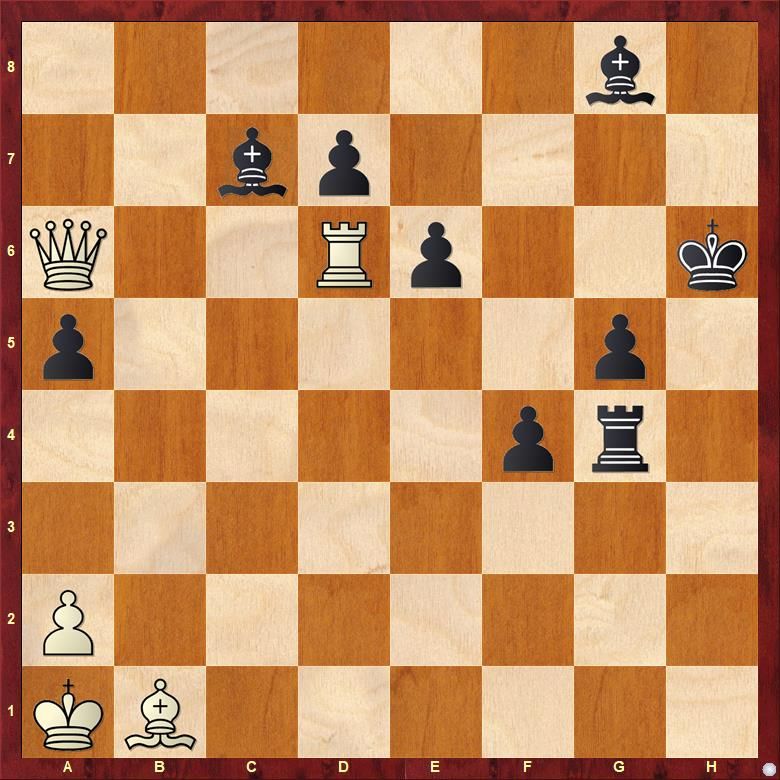
Here's another tricky problem that stumped many of the solvers! The key move of this reflexmate is only 1. Qf1! The idea is to go 2. Ra6, which, by virtue of the reflex condition, would force 2... Be5#. The defences 1... Bb6 and 1... Bxd6 are met with 2. Rd4 Bxd4# and 2. Qa6 Be5#, respectively.
A few of the solvers fell for the try 1. Qa8?, which has the same idea, but is defeated by the tricky 1... Bf7!, which forces White to mate with Qh8—mind you, the reflex condition applies to both sides! Similarly, 1. Rxd7? and 1. Rxe6+? are also tries that fail to 1... Bh7! 2. Rxh7# and 1... Kh5! 2. Rh6#, respectively. Perhaps the most common answer to this problem was 1. Rd1?, but this again is refuted by the simple 1...d6!.
Problem 06
N. Shankar Ram, The Problemist 1983, Commendation

In this problem by India's first IM of chess composition, Narayan Shankar Ram, the key motif seemingly is to block the white queen on the a8-h1 diagonal and go Ng3-h1, forcing gxh1=Q#. However, 1. Rdd5/1. Rbd5 and 1. Rb7, trying to realise this idea, fail to 1... e4 and 1... Bh2, respectively. The solution begins instead with the clever 1. Rd6!. This anticipatorily closes the d6-h2 diagonal and threatens 2. Nxh5 Rxh5#. Only now, the defence 1... e4 is met with 2. Nh1 gxh1=Q#. And for 1... h4, we have 2. Bg8, forcing 2... Rxg3#.
Quite a few solvers wrote 1. Rd1+ Kc2 2. Nxh5 Rxh5# as the solution to this problem. Can you see what is wrong with this idea? Well, here, after 1... Kc2, White must deliver 2. Qa4#. 2. Nxh5 is not legal due to the reflex condition!
Tier II
Problem 07
Anirudh Daga (2023), Original
_GKHFP_708x708.png)
The first thing to observe is that the royal pieces on both sides have swapped places. Some of the solvers wondered whether there was an error in the diagram. Well, there isn't. You must make seven legal moves for both sides to arrive at the position above from the initial game array. Here's the unique solution: 1. e3 d6 2. Qg4 Qd7 3. Qxg7 Kd8 4. Qg4 Qe8 5. Qe2 Bh3 6. Kd1 Bxg2 7. Qe1 Bxf1
Problem 08
Charles Mason Fox, The Problemist Fairy Chess Supplement, 1933
_HJMRJ_708x708.png)
In this one, the game ends with a checkmate with the knight. But where did the knight land to f6 from? Was the last move Ng8-f6#, in which case, could it be that this mating knight is a white pawn that promoted on g8? In chess problem literature, this is a popular theme; it's known as the phoenix: first, a piece is captured, and then the same piece is reborn (like a phoenix!) via pawn promotion! Here's how the game went: 1. f4 e5 2. f5 Bc5 3. f6 Bxg1 4. fxg7 Bxh2 5. Kf2 Ne7 6. Ke3 Rf8 7. g8=N d6 8. Nf6#.
Problem 09
Andrew Buchanan, Retro Mailing List, 2023
_TREKF_708x708.png)
This was a so-called "year problem." The answer is 2023, which many solvers guessed correctly but failed to justify. A bit of math is needed here, but nothing too fancy. First off, we note that the only possible 19 moves to reach this arrangement are d4, h4, Rh3, Rf3, Rf6, f4, f5, Bf4, e3, Bc4, Bd5, c4, Qb3, Qb6, b4, b5, a4, Ra3, Rb3. The next thing to observe is the following 14 moves of these 19: h4, Rh3, Rf3, Rf6, f4, f5, Bf4, e3, Bc4, Bd5, c4, Qb3, Qb6, b4. The thing about this sequence is that it must happen in this exact order. Next, we see that d4 must come before Bf4 is played; this means we can insert d4 in any of the 7 places between h4, Rh3, Rf3, Rf6, f4, f5.


Let us now calculate the number of combinations with d4 fixed at, say, the first position. We will then just have to multiply the resulting number by 7 to come up with the final answer. We can have two cases here, depending on whether Rb3 or b5 is the last move.
Case I (When Rb3 is the last move): If a4 is played in the first move, then we will have 17 ways to play Ra3. Similarly, if a4 is played in the second move, then we will have 16 ways to play Ra3, and so on. In total, we will have 17+16+15+...+1=17(17+1)/2=153 combinations.
Case II (When b5 is the last move): If a4 is played in the first move, then we will have 16 ways to play Ra3. Similarly, if a4 is played in the second move, then we will have 15 ways to play Ra3, and so on. In total, we will have 16+15+14+...+1=16(16+1)/2=136 combinations.
Combining the two cases above, we will thus have 153+136=289 combinations. And now, varying d4 in all seven places we get the final answer as 7 times 289, which equals 2023!
Problem 10
Alberto Armeni, Buletin Problemistic, 2018
_EX6PN_708x708.png)
As in Helpmates, the key to solving series movers lies in visualising the final position of the solution. In the above problem, the black units don't move at all. Therefore, to checkmate the black king on d6, which has as many as six flight squares, White needs to promote both their pawns. To do so, the knight on d8 and the pawn on f6 have to be eliminated. It is up to the white king to realise these goals. It has to carry out a long journey. But how exactly? Here's the solution: 1. Ke3 2. f4 3. f5 (closing the bishop's line) 4. Kd3 5. Kc3 6. Kb4 7. Kb5 8. Ka6 9. Ka7 10. Kb8 11. Kc8 12. Kxd8 13. Ke8 14. d8=B (underpromotion is necessary; d8=Q puts the black king under check and is illegal) 15. Bxf6 16. Bd4 17. f6 18. f7 19. f8=R (again, f8=Q is illegal) 20. Rf6#.
Problem 11
Jean Zeller, feenschach, 1972
_RDYPA_708x708.png)
This one was probably the most entertaining and humorous of all the chess compositions in the two tiers combined. The white pawns d4, d6, and h6, surrounding Black's king, cover three out of its eight flight squares. How do we cover the remaining squares? 1. c1=N 2. Nxe2 3. Ng6 4. e2 5. e1=N 6. Nxg2 7. Ne6 8. g2 9. g1=N 10. Nxh3 11. Nf7 12. h3 13. h2 14. h1=N 15. Nf5—Black blockades four more squares with Nightriders, and this allows 15... Ne4#.
_QBQDJ_708x708.png)
Problem 12
Harry Fougiaxis, Sinfonie Scacchistiche, 1988
_QTPXQ_708x708.png)
Harry Fougiaxis is an International Master of chess composition from Athens, Greece. He is not only a world-class expert in helpmates but has also formerly served as the President of the World Federation for Chess Composition (WFCC). The solutions are 1.Ge7 Sg5 2.Ge2 Sce4# and 1.Gb6 Sb3 2.Gf2 Sed4#. Vlaicu Crisan, an IM of both solving and composing, who was one of our participants (and is also now in the leaderboard), wrote: "Not surprisingly, this is my favorite! The key moves seem rather surprising once you have seen the set play. Two double check mates in orthogonal diagonal correspondence!"
The Tiebreaker
The tiebreaker will consist of 15 problems that the contestants must solve in real-time. They will have approximately 5 minutes to solve each problem. The event will be held on a game-based learning platform, either Kahoot or Quizizz; hence, the questions will be either multiple-choice or one-word answer types.
Speaking of the problems, they will be a mixed bag of orthodox and unorthodox types. About half of them will be retroanalytic questions concerning the deduction of legal last moves, the colour of units, adding and removing units, and so on. The rest will include selfmates, reflexmates, and directmates. There will be no helpmates. The contestants will either have to write down the key or, in case of a long problem, the last move of the mainline.
The event will take place on January 14th from 2 pm (IST) onwards and will be streamed live on YouTube. The contestants must remain on camera the entire time and must not have any assistance. They can use a board to set up positions, but no digital tools for this purpose will be allowed. A separate email will be sent to all finalists well before January 14th as confirmation. In the meantime, any further queries/communications can also be directed to chessbaseindiasocial@gmail.com.
Acknowledgement
We thank Mu-Tsun Tsai. His FEN tool was used to create the diagrams for the second tier of our contest.
Links to Previous Articles
2. Math, Magic, and Mystery on the Chessboard—Winter Solving Tier II












































